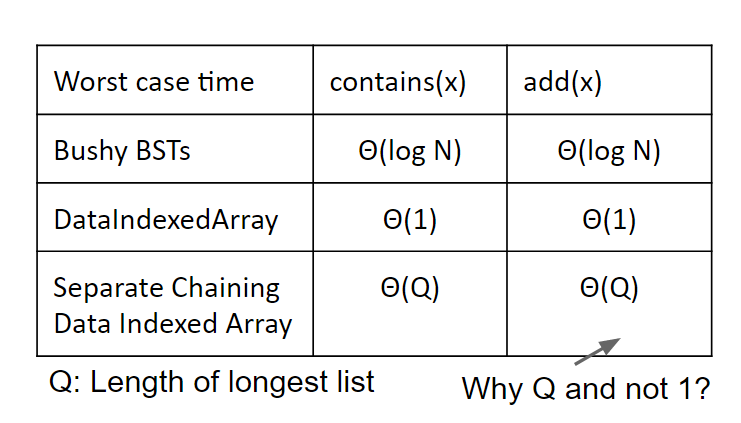
Data Indexed Arrays
Sets
经过很多节课的学习,我们发掘了SET/MAP ADT的不同实现方式:
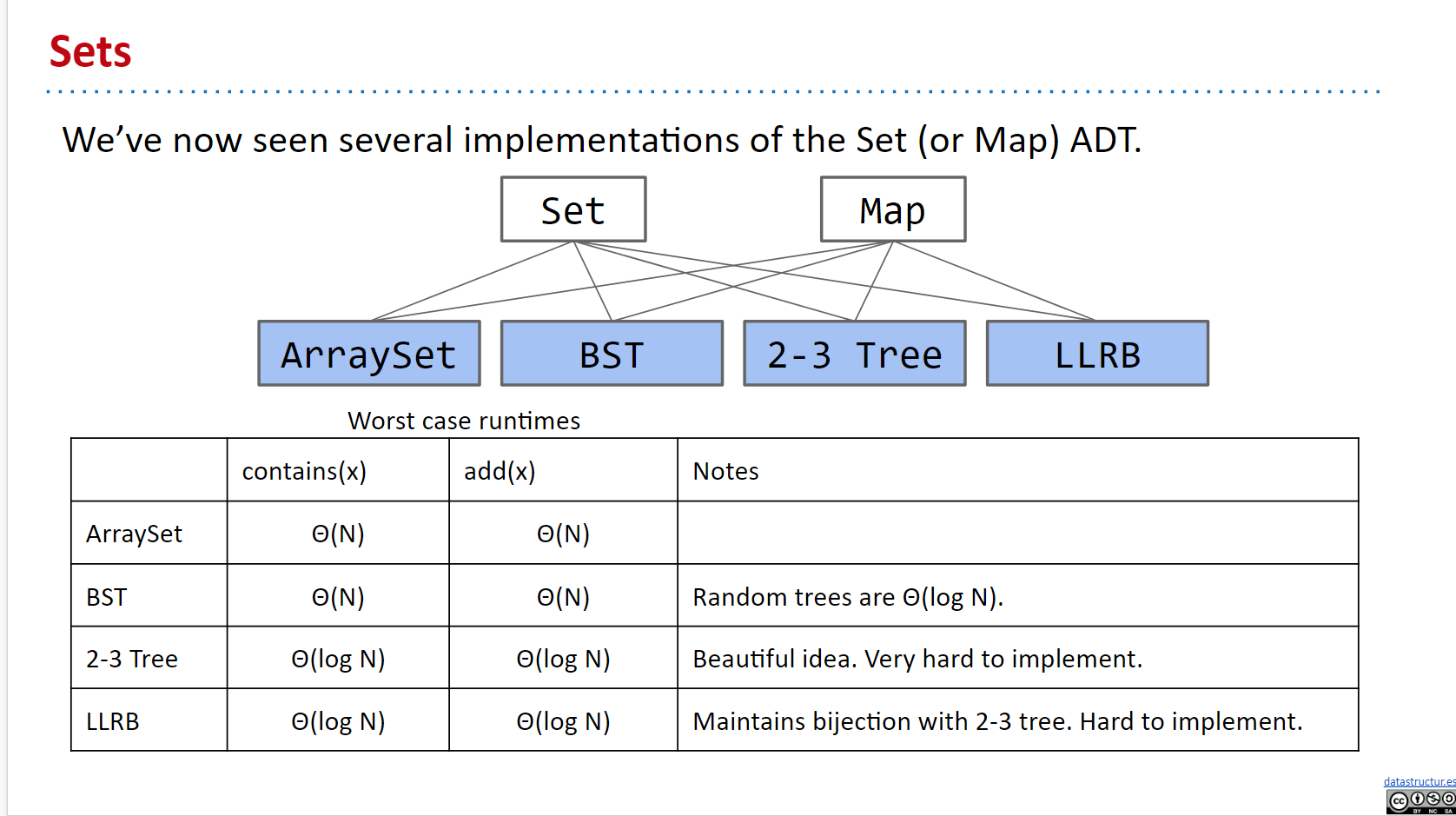
但是对于 Search Tree Based Sets 的数据结构来说,还是存在不少的问题:
Limits of Search Tree Based Sets
Limits of Search Tree Based Sets:
- Our search tree based sets require items to be comparable. 我们的树需要能比较(comparable),若是不用比较就好了
- Need to be able to ask “is X < Y?” Not true of all types.
- Could we somehow avoid the need for objects to be comparable?
- Our search tree sets have excellent performance, but could maybe be better? 能否于时间上更近一步
- Θ(log N) is amazing. 1 billion items is still only height ~30.
- Could we somehow do better than Θ(log N)?
我们都知道这俩问题的答案都是 yes
Using Data as an Index
如图所示:
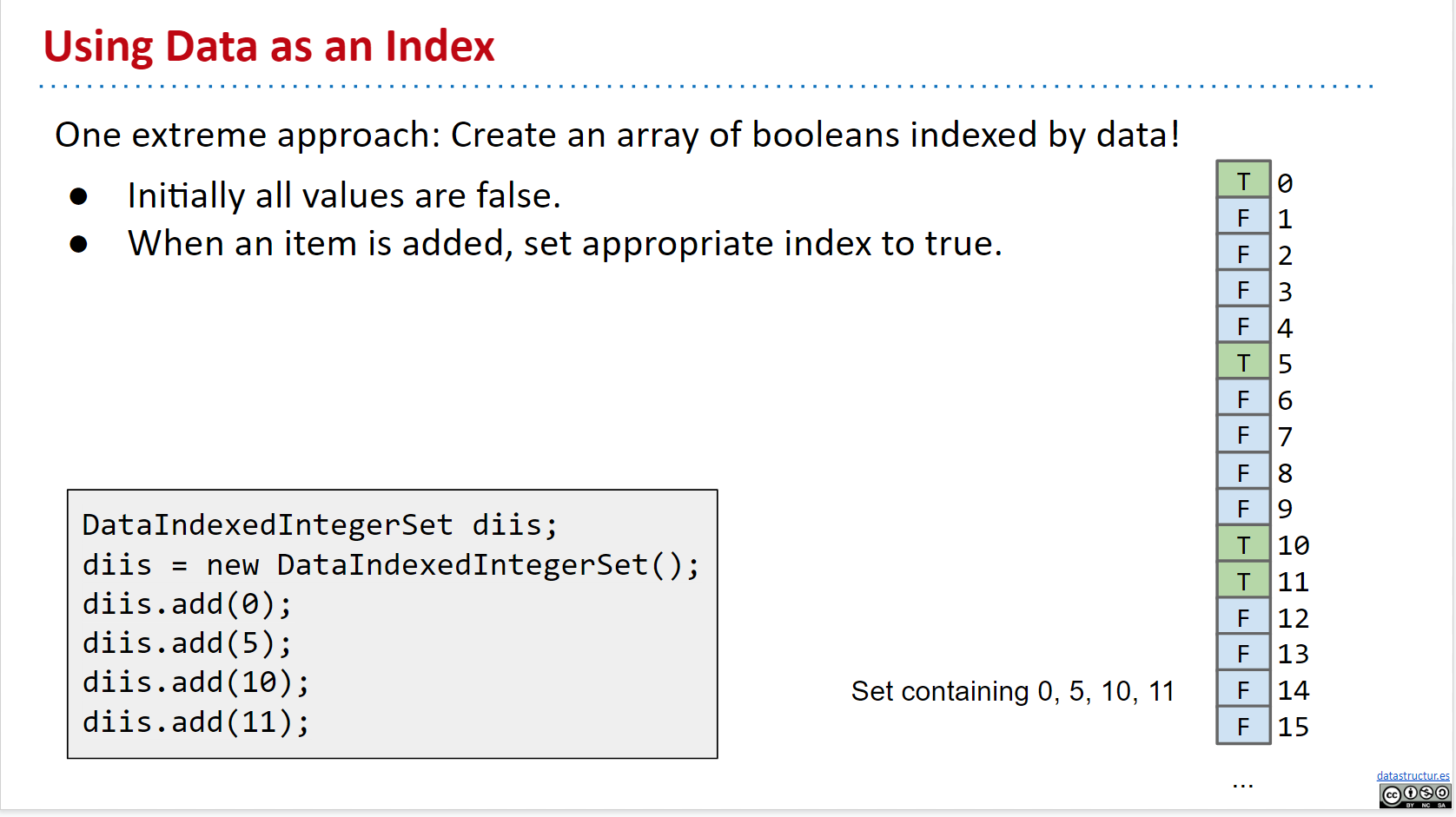
首先我们建立一个奇怪的 bool 数组被叫做:a data indexed integer set
- O(1)
- 没有比较
- 但是浪费 memory
- 需要泛化
DataIndexedEnglishWordSet
上面的例子只能存储数字,我们如何存储英文单词呢:用数字代表字母,但为了 Avoiding Collisions 避免冲突,我们需要做如下的操作(pattern):
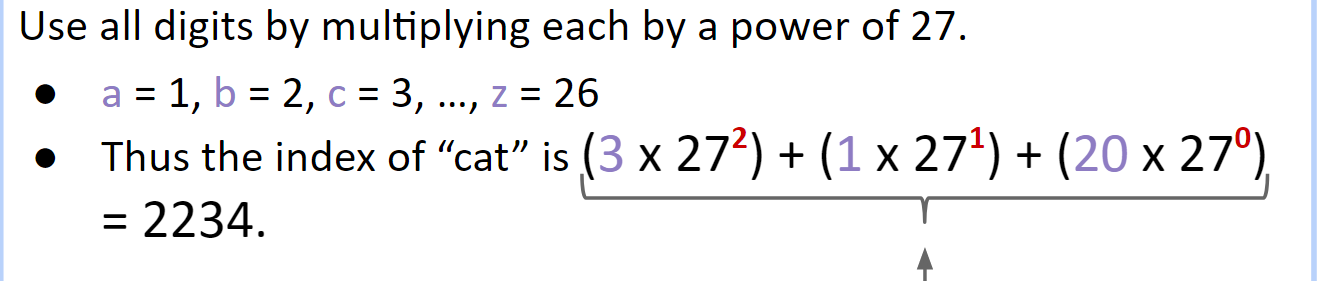
27进制
27 进制只能涵盖英文小写数字,我们使用 ASCII 码可以使其覆盖更大的范围(33 -126)
当然,要是我们举行扩大,我们可以涵盖更多的语言文字
Integer Overflow and Hash Codes
随着字符集的扩大,明显我们会 Overflow,显然不合适
Via Wolfram Alpha: a hash code “projects a value from a set with many (or even an infinite number of) members to a value from a set with a fixed number of (fewer) members.”
由于鸽巢原理,以有穷来表示无穷是必然会冲突的,那么问题就变成了:
- collision handling : How do we resolve hashCode collisions
- computing a hashCode:How do we compute a hash code for arbitrary objects
Hash Tables: Handling Collisions
如何解决冲突:
Instead of storing true in position h, store a “bucket” of these N items at position h.
我们用 桶 替代布尔值
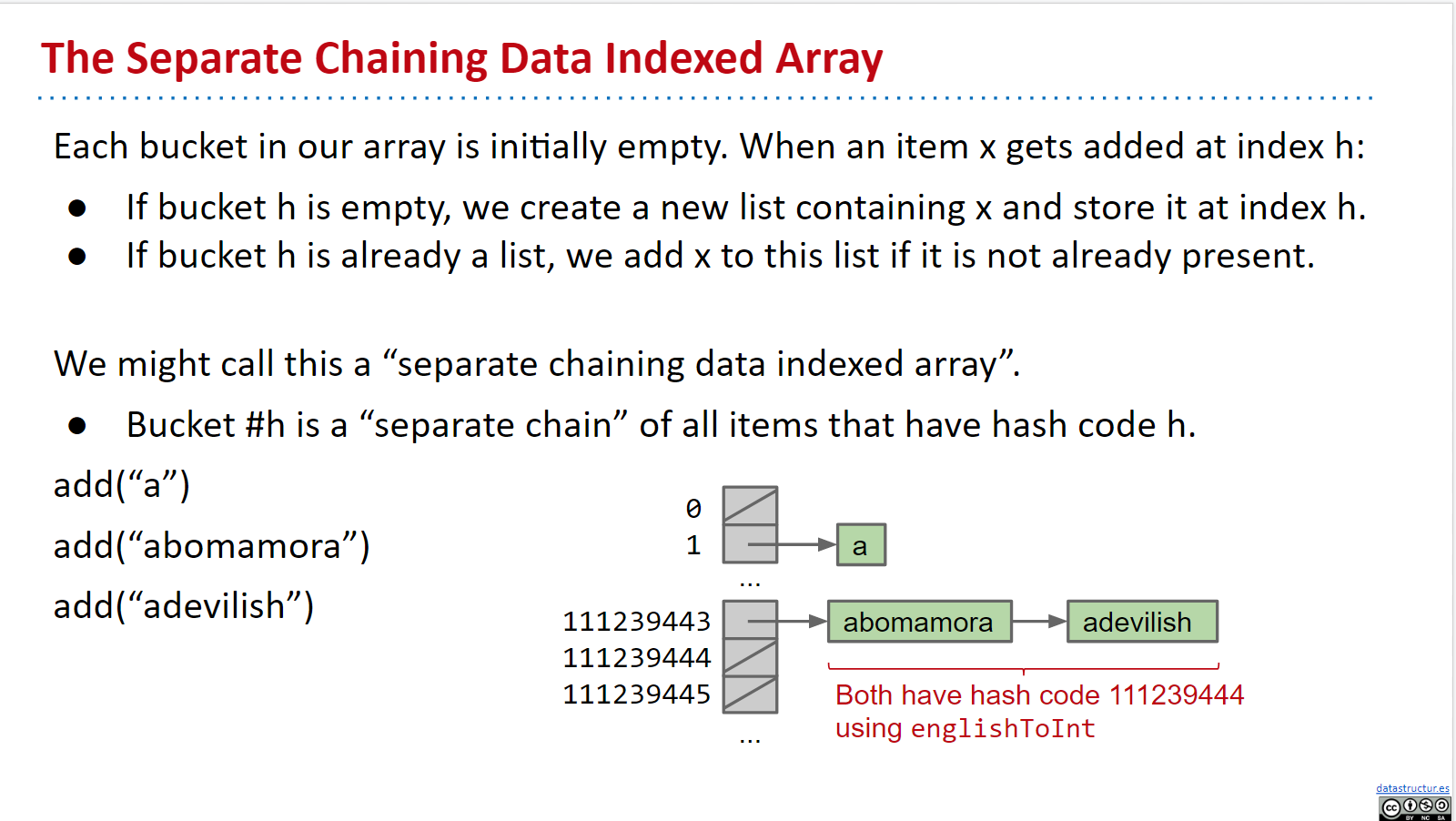
 然而,由于我们的桶数是有限的,所以并不能做到
然而,由于我们的桶数是有限的,所以并不能做到O(1)的时间复杂度,于是我们进行一番改进(reszing):
- An increasing number of buckets M.
- An increasing number of items N.
- When N/M is ≥ 1.5, then double M.
思想是:太挤了!加桶!
总结如下:
Assuming items are evenly distributed (as above), lists will be approximately N/M items long, resulting in Θ(N/M) runtimes.
注意这里的假设是 items 是均匀分布的
- Our doubling strategy ensures that N/M = O(1).
- Thus, worst case runtime for all operations is Θ(N/M) = Θ(1).
- … unless that operation causes a resize.
当然,每当我们 resize 后,都需要重新计算我们的哈希表,这也导致了 resize 的时间复杂度要进行考量:
One important thing to consider is the cost of the resize operation.
- Resizing takes Θ(N) time. Have to redistribute all items!
- Most add operations will be Θ(1). Some will be Θ(N) time (to resize).
- Similar to our ALists, as long as we resize by a multiplicative factor, the average runtime will still be Θ(1).
- Note: We will eventually analyze this in more detail.
HashTable in Java
Java 里分为:java.util.HashMap and java.util.HashSet.
然而我们并不需要 implements Hashable,因为 all objects in Java must implement a .hashCode() method.
PS:Default implementation simply returns the memory address of the object.
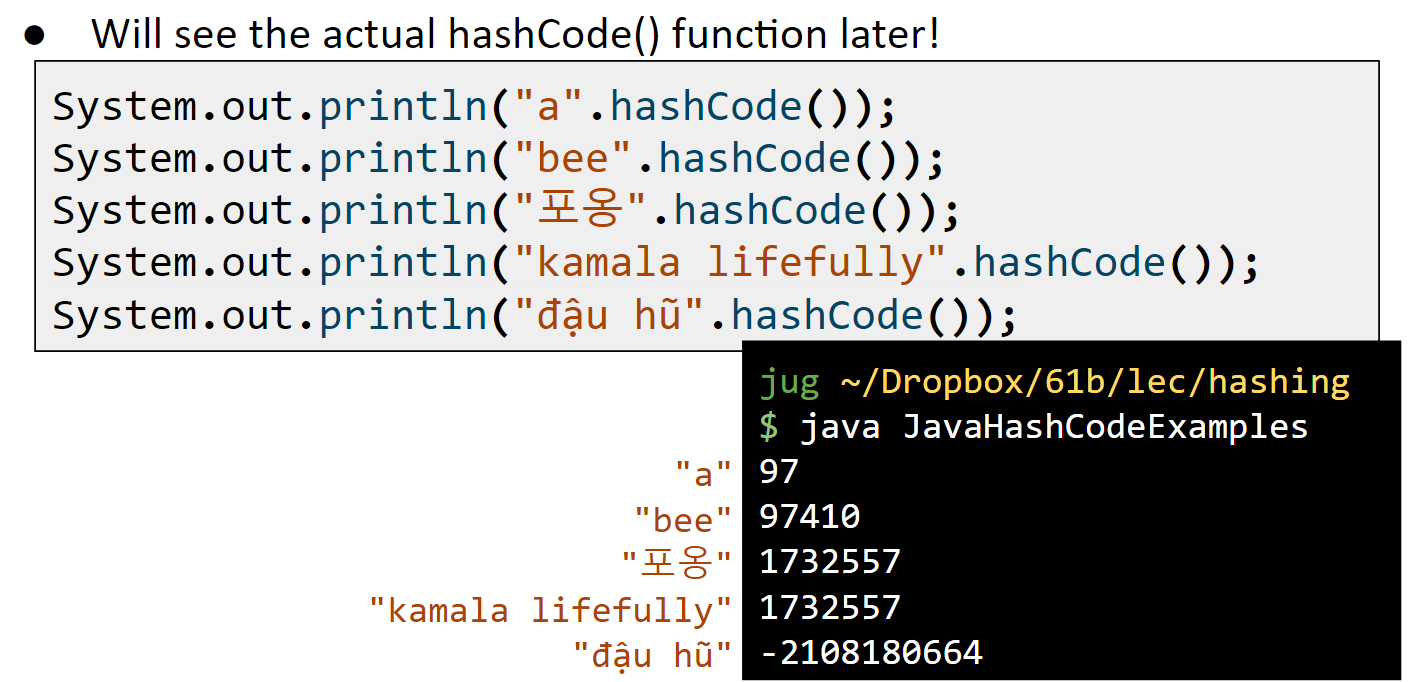
但是我们注意到,java 中出现了负数的 HashCode:
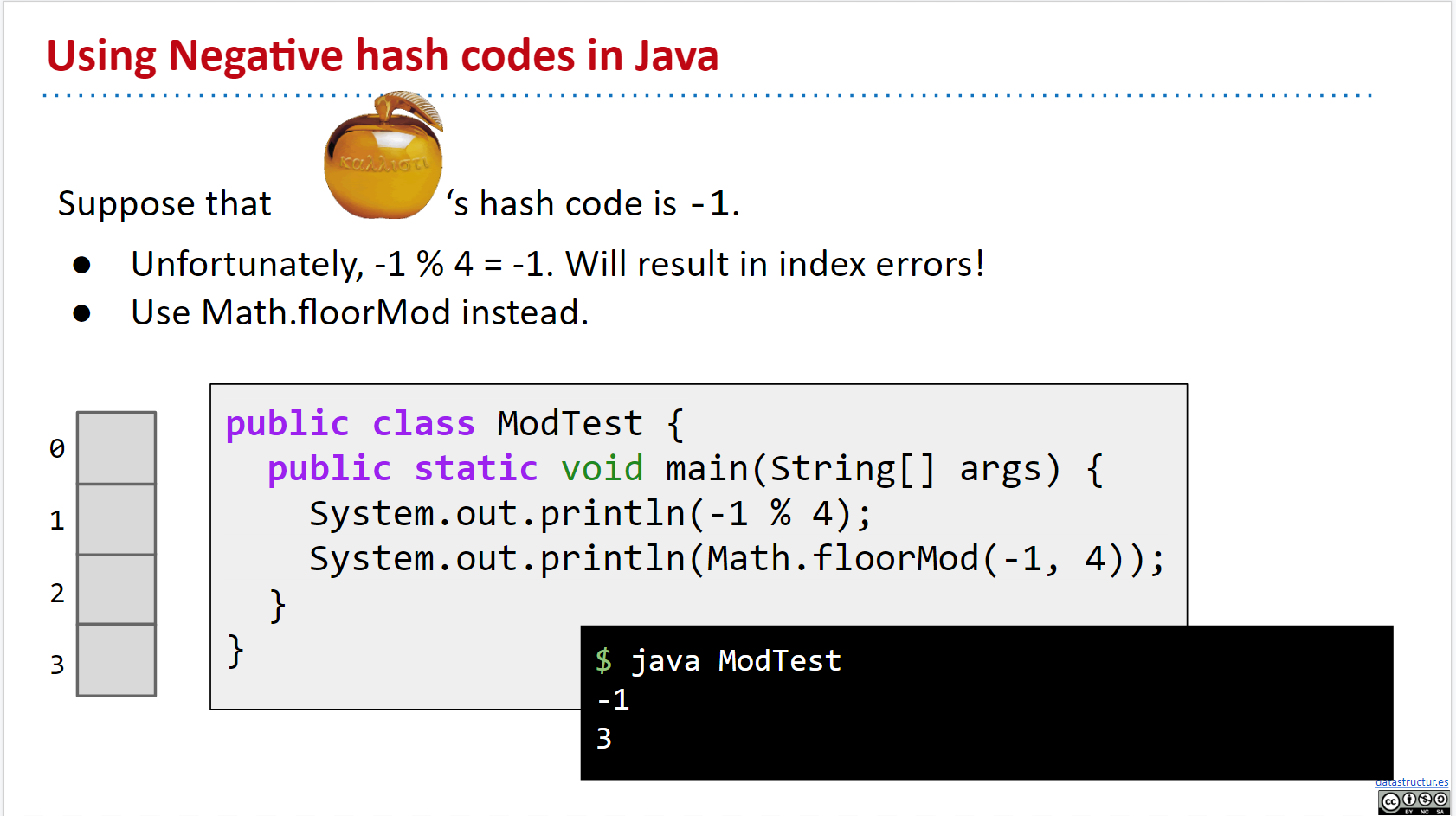
如何处理负数?使用 Math.floorMod():
顺便一提,讲了在使用中的一些规范:
Warning #1: Never store objects that can change in a HashSet or HashMap!
- If an object’s variables changes, then its hashCode changes. May result in items getting lost.
Warning #2: Never override equals without also overriding hashCode.
- Can also lead to items getting lost and generally weird behavior.
- HashMaps and HashSets use equals to determine if an item exists in a particular bucket.
- See study guide problems.
Good HashCodes (Extra)
如何写一个好的哈希函数?
Can think of multiplying data by powers of some base as ensuring that all the data gets scrambled together into a seemingly random integer.
可以将数据乘以某个基数的幂
下面是 java8 中 hashCode的实现:
@Override
public int hashCode() {
int h = cachedHashValue;
if (h == 0 && this.length() > 0) {
for (int i = 0; i < this.length(); i++) {
h = 31 * h + this.charAt(i);
}
cachedHashValue = h;
}
return h;
}
- 31:对 hashcode 来说其大数字会更好(126 ASCII),但是 126 会导致:Any string that ends in the same last 32 characters has the same hash code.Because of overflow