14.1 Dynamic Connectivity and the Disjoint Sets Problem
本节讲的是 “union-find” 算法,中文翻译就很熟悉了:并查集
14.1.1 The Disjoint Sets Data Structure
上来那开宗明义,啥是并查集啊!
The Disjoint Sets data structure has two operations:
- connect(x, y): Connects x and y.
- isConnected(x, y): Returns true if x and y are connected. Connections can be transitive, i.e. they don’t need to be direct.
并查集只有两个操作:
- 合并/连接
- 查询
public interface DisjointSets {
void connect(int p, int q);
boolean isConnected(int p, int q);
}14.1.2 The Naive Approach
这个其实没意思,就是这个 API 它用了会是啥效果

14.2 Quick Find
如何实现呢:
若尝试 Map , Slow because you have to iterate to find which set something belongs to.
这里其实的意思是,我们选择的底层的实现方式是会影响效率的,国内的挨过数据结构毒打的同学就悟了:这就是所谓的逻辑结构和物理结构嘛,不同物理结构是实现会导致不同的操作呗
14.2.1 SETS
Idea #1: List of sets of integers, e.g. [{0, 1, 2, 4}, {3, 5}, {6}] : List>.
初始化 : [{0}, {1}, {2}, {3}, {4}, {5}, {6}]
若是要查找 :Requires iterating through all the sets to find anything. Θ(N).
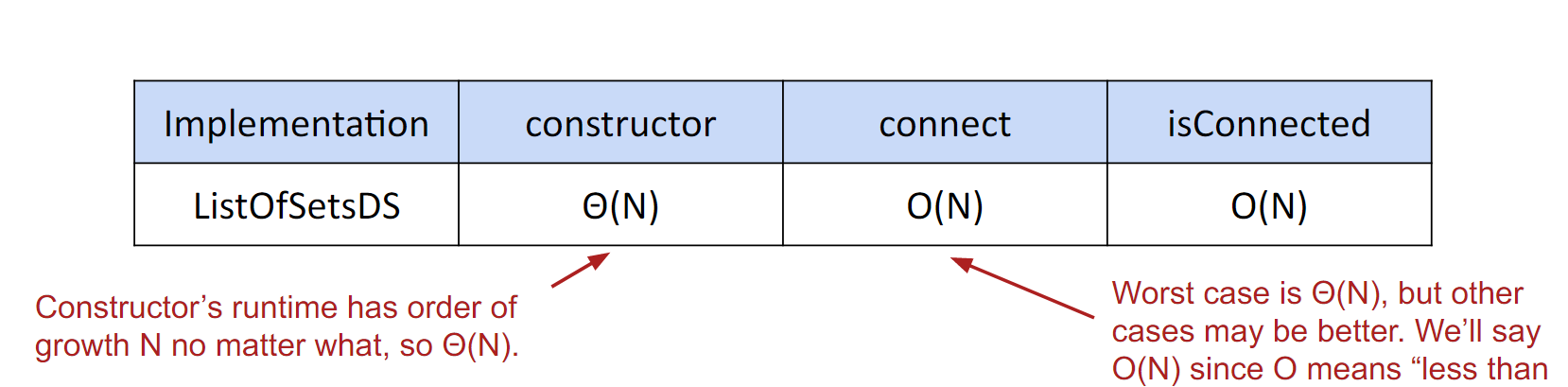
Important point: By deciding to use a List of Sets, we have doomed ourselves to complexity and bad performance.
用错了实现数据结构,导致了这样的情况
14.2.1 LIST
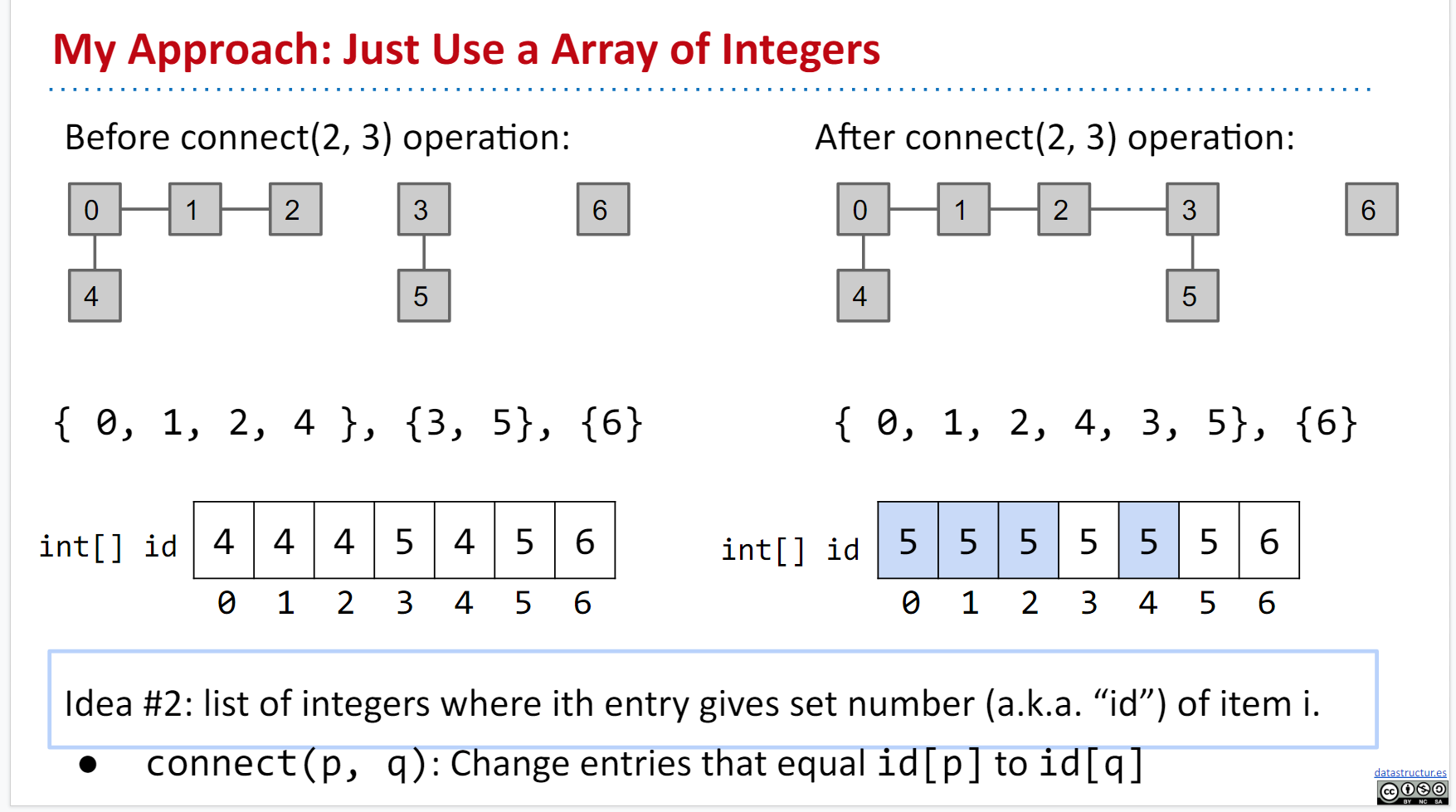
Idea #2: list of integers where ith entry gives set number (a.k.a. “id”) of item i.
这个的意思是:将 int[x] 指向其根节点
package lec14_Disjiont_Sets;
public class QuickFindDS implements DisjointSets {
private int[] id;
@Override
public boolean isConnected(int p, int q) {
return id[p] == id[q];
}
@Override
public void connect(int p, int q) {
int pid = id[p];
int qid = id[q];
for (int i = 0; i < id.length; i++) {
if (id[i] == pid) {
id[i] = qid;
}
}
}
// 初始化,所有的元素都是独立的
public QuickFindDS(int N) {
id = new int[N];
for (int i = 0; i < id.length; i++) {
id[i] = i;
}
}
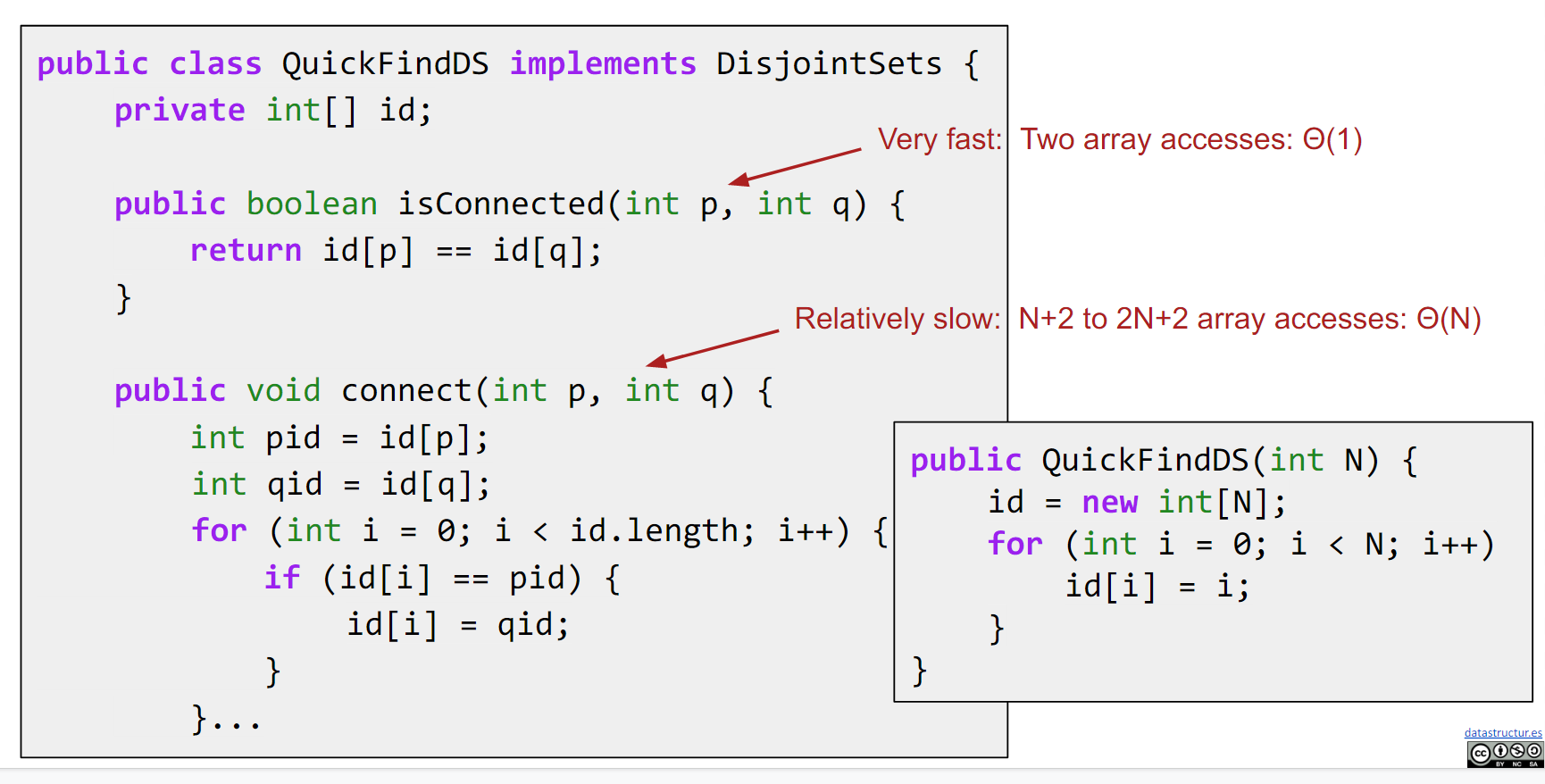
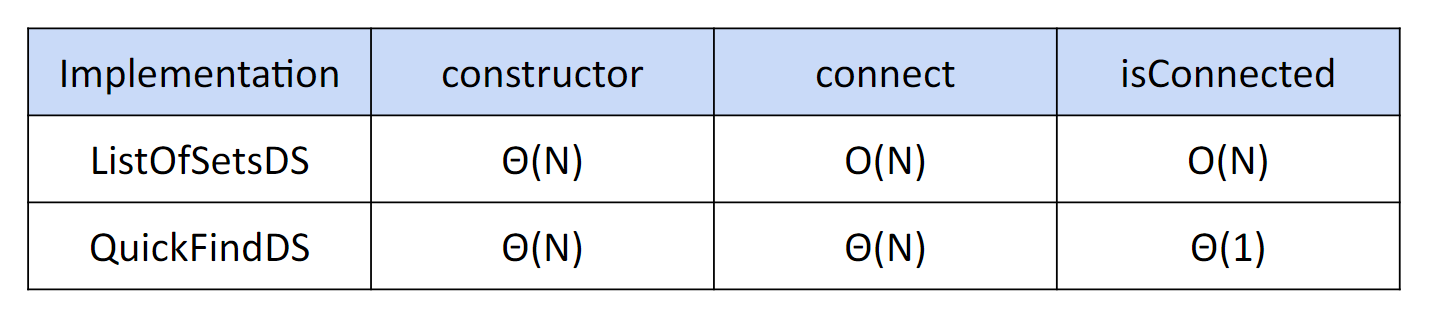
}这里需要强调的是:
虽然 isConnected 是极快的,但是 connect 是很慢的,为什么,那每次遍历都往祖坟上刨肯定慢啊
14.3 Quick Union
为了解决 connect 的速度问题,我们要进行一个改进
跳过那些巴拉巴拉的东西,让 int[x]指向其父节点而不是root,而root节点值为 -1
package lec14_Disjiont_Sets;
public class QuickUnionDS implements DisjointSets {
private int[] parent;
public QuickUnionDS(int n) {
parent = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
}
}
private int find(int p ){
int r = p;
while (parent[r] >=0 )
{ r = parent[r]; }
return r;
}
@Override
public void connect(int p, int q) {
int i = find(p);
int j = find(q);
parent[i] = j;
}
@Override
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
}
14.4 Weighted Quick Union
略,其实是油管的翻译有问题了,而且这玩意我考研不考
14.5 Path Compression (CS170 Preview)
略
ACWING
并查集:
- 将两个集合合并
- 询问两个元素是否在一个集合当中
暴力存储:
尝试数组存储 :belong[x] = a (x的集合)
if(belong[x] == belong[y]) O(1)
但是合并那是及其耗时的,怎么办呢:
基本原理:
用树的形式维护所有集合,每一个集合用一棵树维护,其编号为根节点的编号,对每一个点都存储其父节点p[x]
- 如何判断树根: if[p[x] == x]
- 如何求 x 的集合编号 :while(p[x]≠x) x = p[x]; //这里会导致高时间复杂度
- 如何合并两个集合:一个根做另一个根的子节点 p[x] = y
对 2. 的优化,每次找到之后,将路径上的所有点都指向根节点(所谓的路径压缩)
还有一个优化:按秩合并?还有 路径减半 路径分裂吗,但是关我屁事,会用路径压缩写就完事了
836. 合并集合
一共有 nn 个数,编号是 1∼n1∼n,最开始每个数各自在一个集合中。
现在要进行 mm 个操作,操作共有两种:
M a b,将编号为 和 的两个数所在的集合合并,如果两个数已经在同一个集合中,则忽略这个操作; a a b bQ a b,询问编号为 和 的两个数是否在同一个集合中; a a b b
输入格式
第一行输入整数 nn 和 mm。
接下来 mm 行,每行包含一个操作指令,指令为 M a b 或 Q a b 中的一种。
输出格式
对于每个询问指令 Q a b,都要输出一个结果,如果 aa 和 bb 在同一集合内,则输出 Yes,否则输出 No。
每个结果占一行。
数据范围
1≤n,m≤1051≤n,m≤105
输入样例:
4 5
M 1 2
M 3 4
Q 1 2
Q 1 3
Q 3 4输出样例:
Yes
No
Yes#include "iostream"
using namespace std;
const int N = 100010;
int p[N];
int n,m;
int find(int x) // return x的root + 路径压缩
{
if(p[x]!= x) p[x] = find(p[x]);
return p[x];
// return p[x] == x ? x : p[x] = find(p[x]);
}
int main()
{
cin>>n>>m;
for (int i = 1; i <= n; i ++ ) p[i] = i;
while (m -- ){
// char op[2];
char c;
int a,b;
// cin >>op>>a>>b;
cin >>c>>a>>b;
// if(op[0] == 'M') p[find(a)] = find(b);
if(c == 'M') p[find(a)] = find(b);
else {
if (find(a) == find(b)) puts("Yes");
else puts("No");
}
}
return 0;
}